[最も選択された] 四 角錐 の 公式 125432-四角錐の公式

公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成

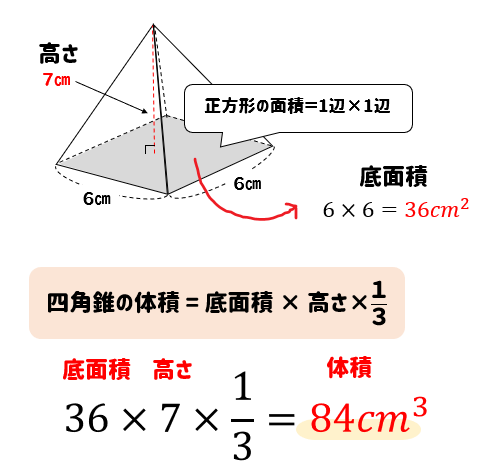
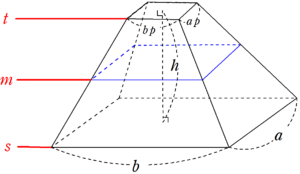
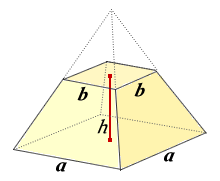
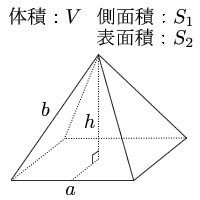
 まとめ：正四角錐の体積の求め方も大丈夫！ 正四角錐の体積の公式はどうだった？ ？ 底面積×高さ×1/3 という計算をゆっくりしてみてね。 テスト前に復習しておくと心強いかも！ そんじゃねー Ken横 b と d ）が並行であり， 高さ h の四角錐台 （稜線は 1 点で交わらなくてもよい） （付図 1） の体積：

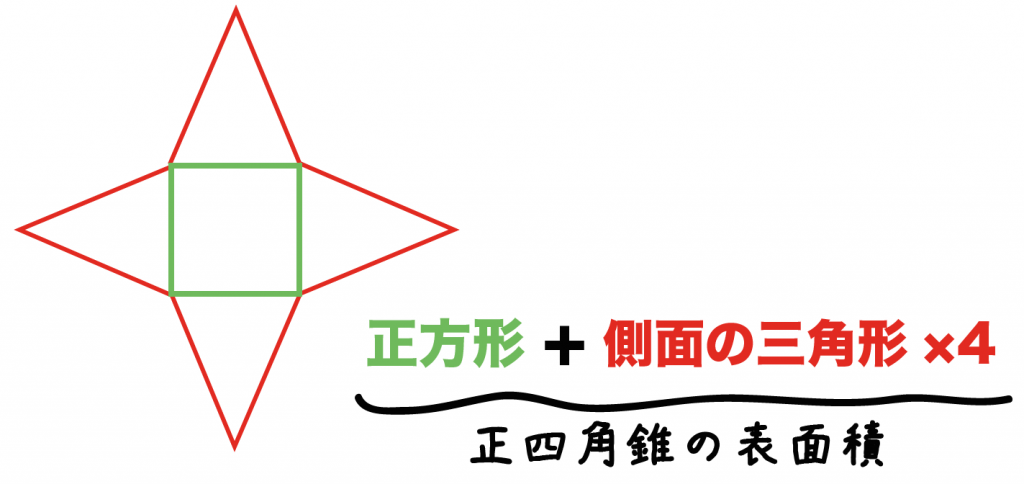
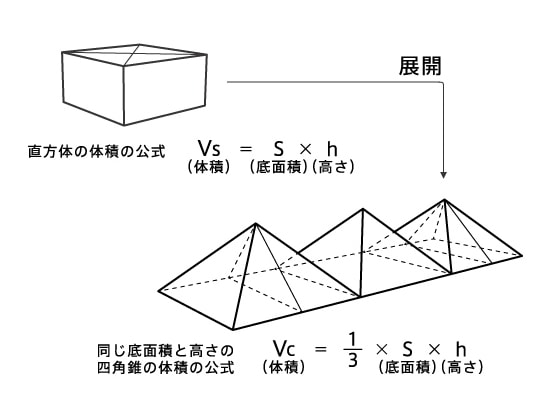
四角錐の公式

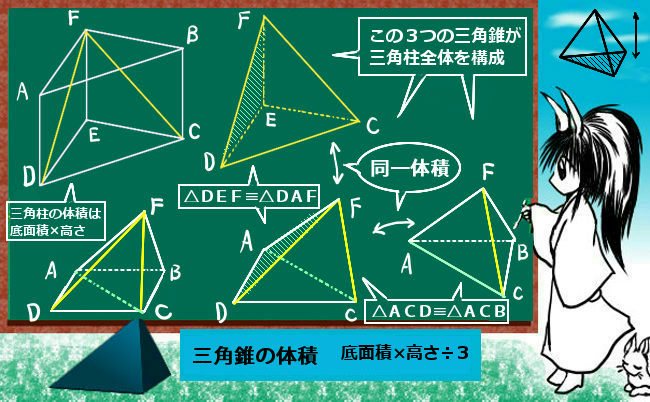
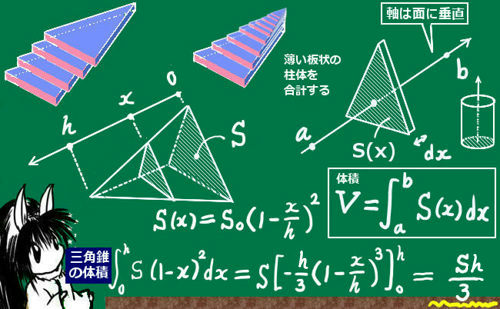
四角錐の公式- 積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない（円錐でも三角錐でも四角錐でも適用可能）証明方法です。 三角錐の公式が使えるので、 円錐の体積＝底面積×高さ／3 になることがわかります。 （別の例） 上図のように、立方体を考えます。 立方体の中心の点を頂点とし、立方体の1つの面を底面とする図形は 高さが立方体の辺の長さの半分の四角錐です。

高中 B4 1 1 兩面角 四角錐 尹正數學 Youtube

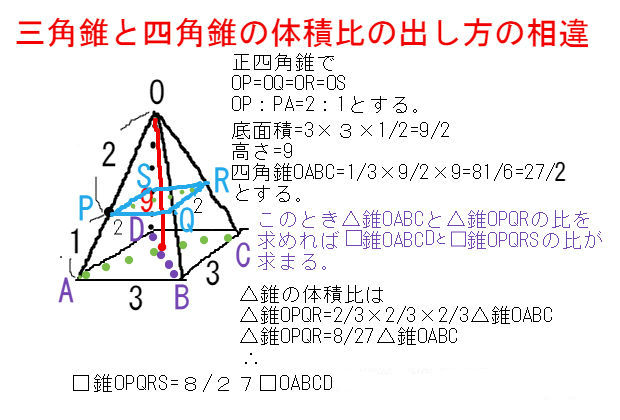
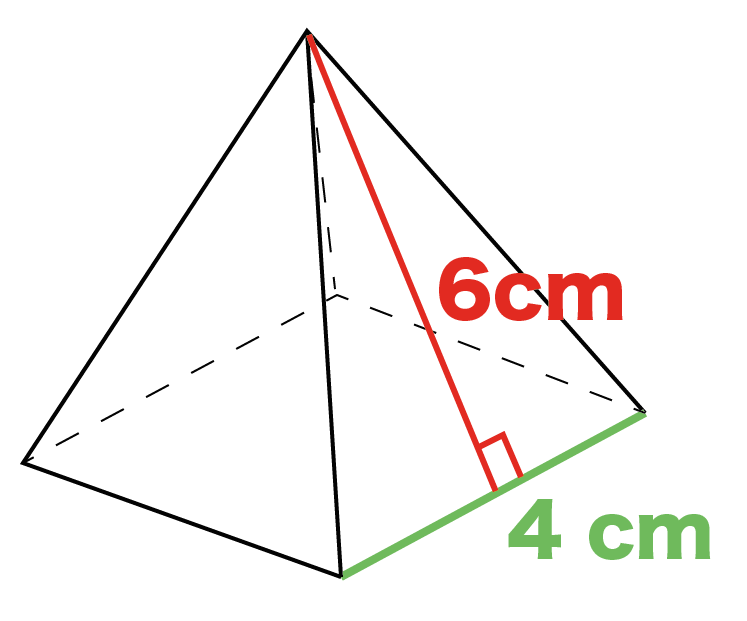
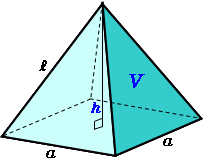
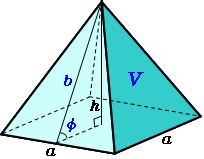
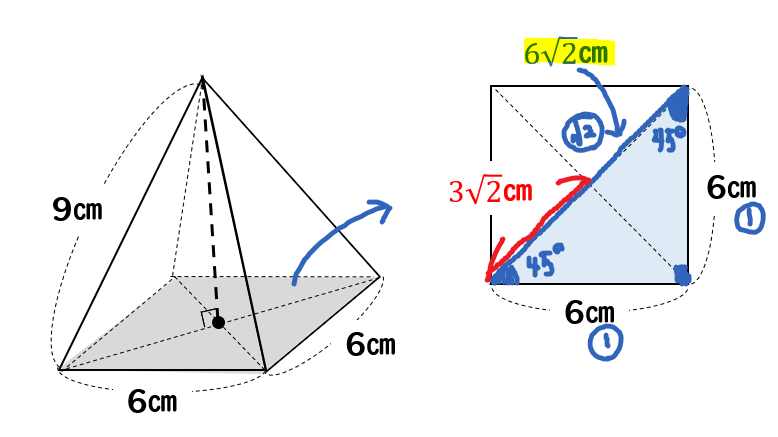
なお，六辺の長さが全て求まっているときには余弦定理により角度（ cos ⁡ \cos cos ）が簡単に求まるので，この公式を使えば 六辺の長さから四面体の体積を機械的に求めることもできます。 証明の前に例題です。この公式，一見かなりマニアックですが，意外と検算に使えます。四角錐の体積＝(35)÷2×4×6÷3＝32cm 3 です。 角錐の体積の公式は？1分でわかる公式、柱体の体積との違い、3分の1になる証明 錐体（円錐、角錐）の体積は、底面積が S S 、高さが h h の錐体の体積 V V は以下の式で表します。 V = 1 3Sh V = 1 3 S h この公式を学習したときに 1 3 1 3 になる理由は知らなかったと思います。 これは特殊な四角錐の場合には比を用いて簡単に証明することが

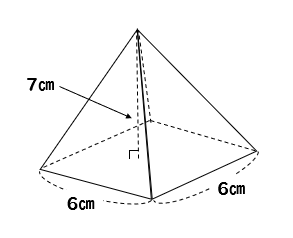
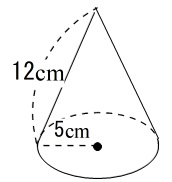
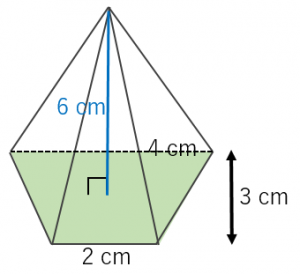
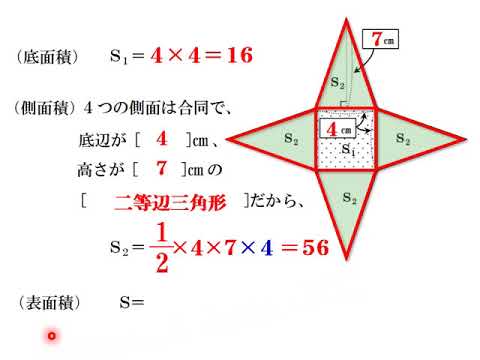
角錐の体積の公式は？ 角錐の体積の公式は 底面積×高さ×3分の1（又は、底面積×高さ÷3） です。角錐は底面が多角形の錐体です。三角錐、四角錘、円錐など色々な形状がありますが、体積の公式は全て同じです。 下図の三角錐の体積を算定しましょう。 角錐の体積について！ 四角錐の問題です 縦4センチ横4センチで、高さが7センチの四角錐の体積を求めよ 16×7÷3という式で合っていますか？ 割り切れないのですが・・＞＜ 至急お願いの体積 V = 4 3πr3 V = 4 3 π r 3 体積 = 4 × 314 × 半径 × 半径 × 半径 ÷ 3 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 球の体積の求め方 」をご覧ください。 球の体積の求め方

四角錐の公式のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

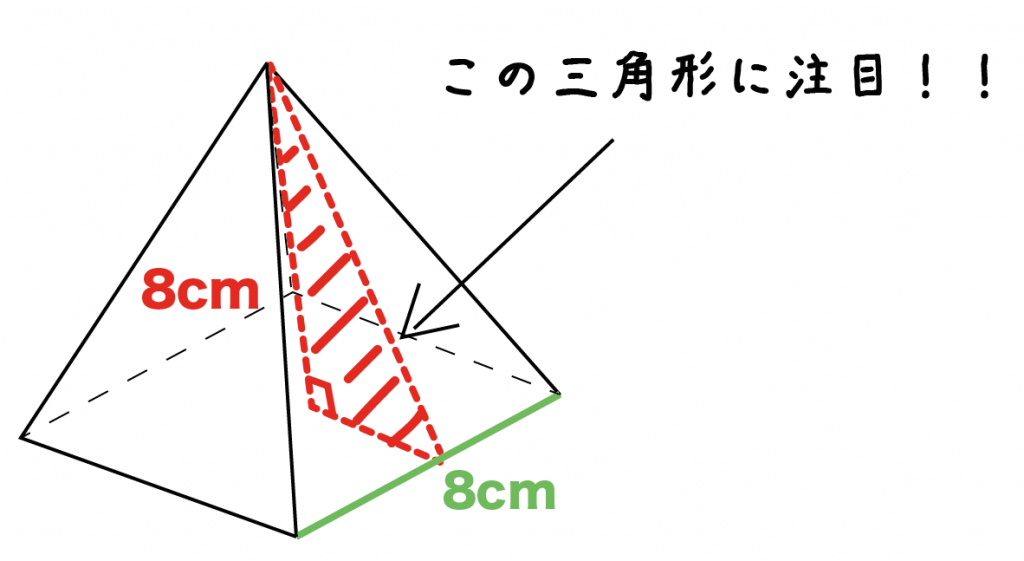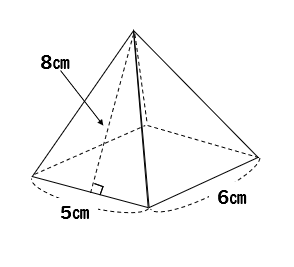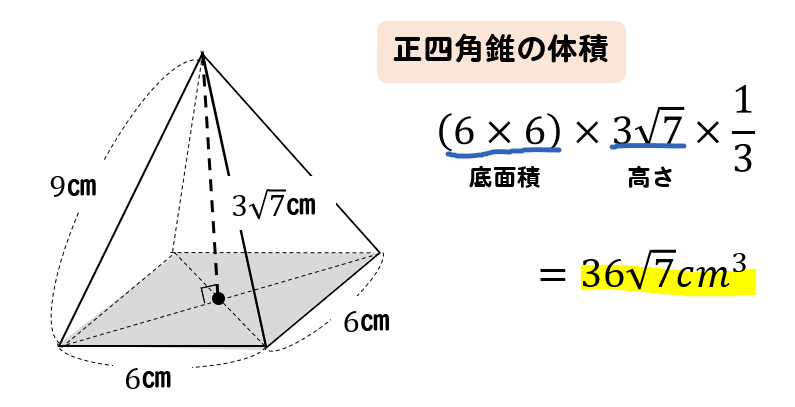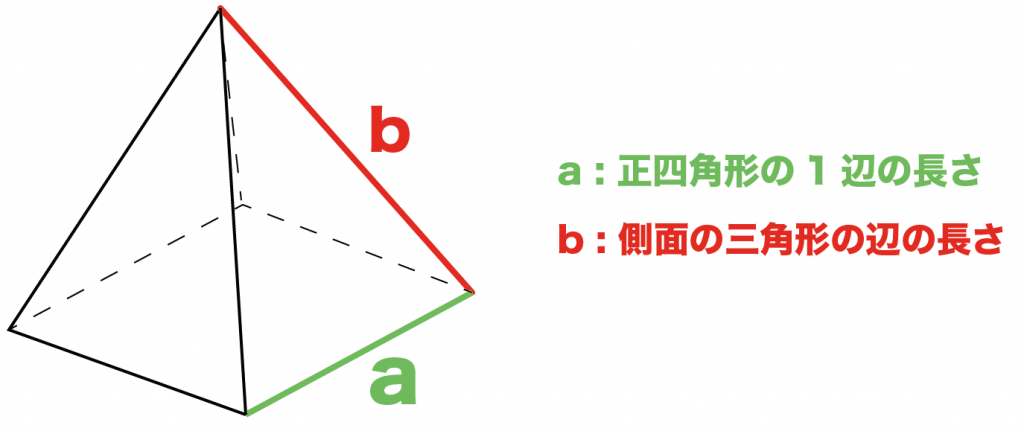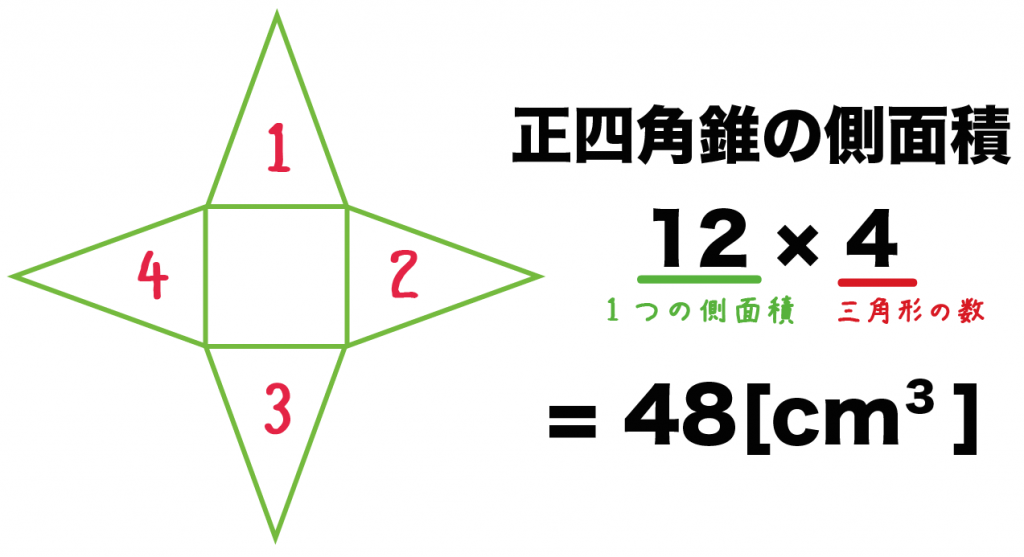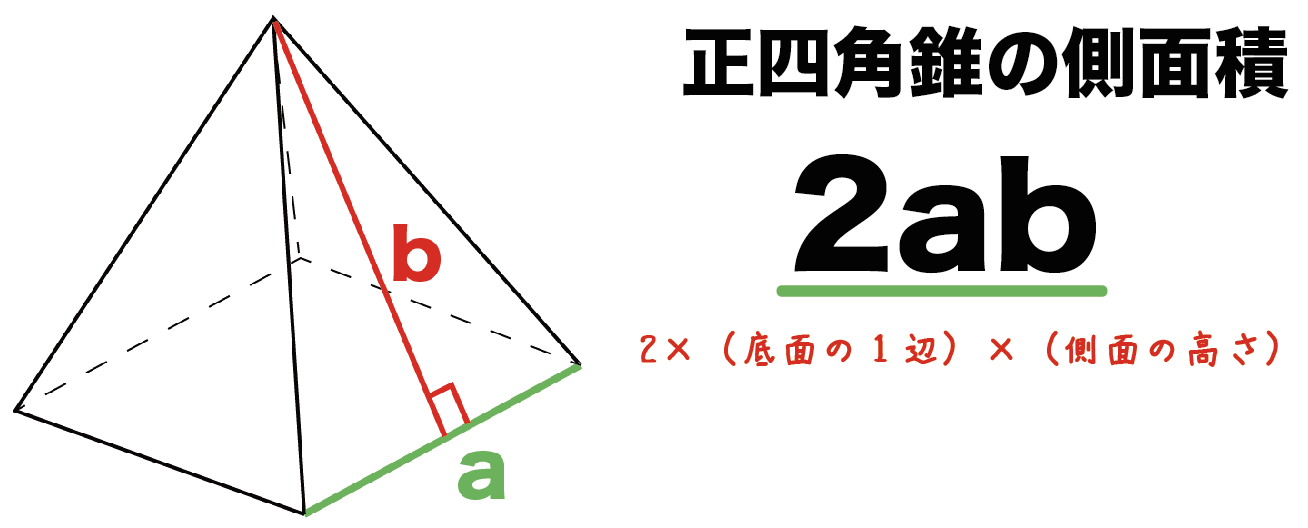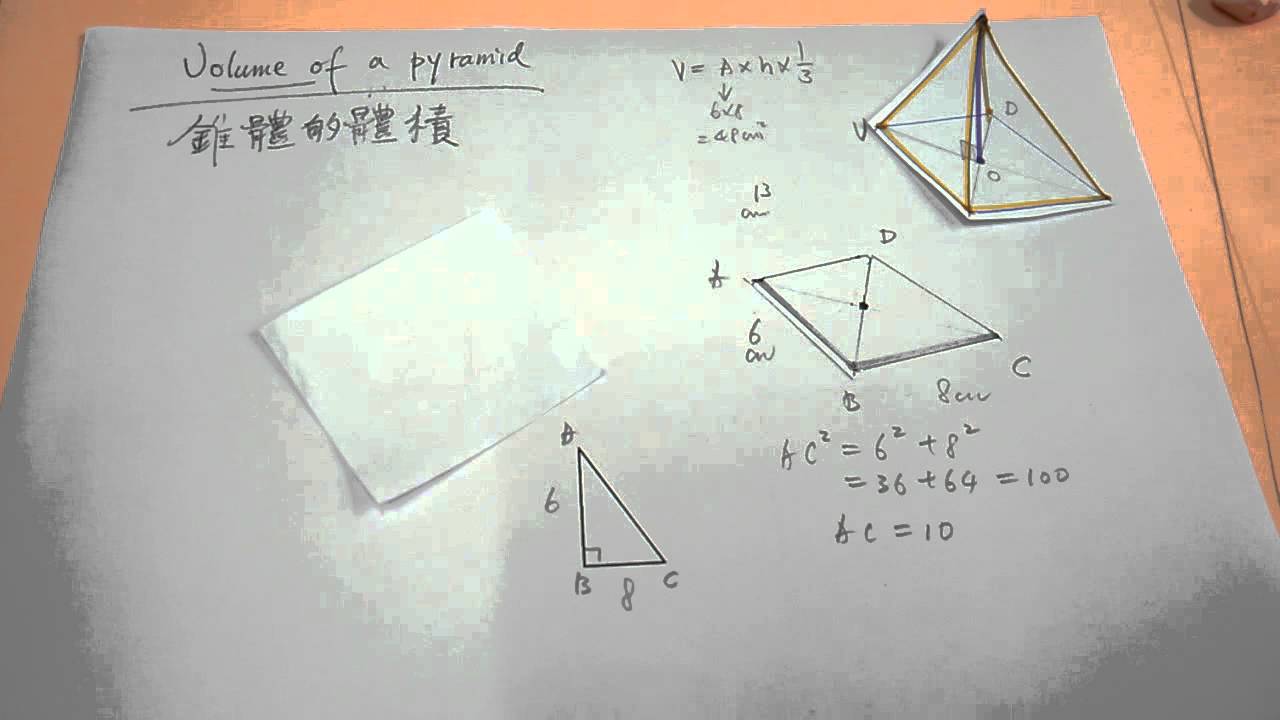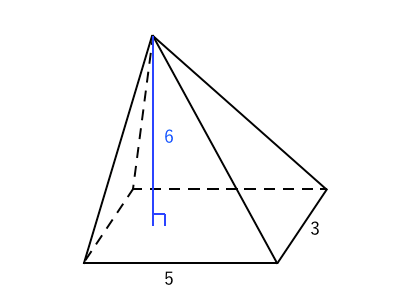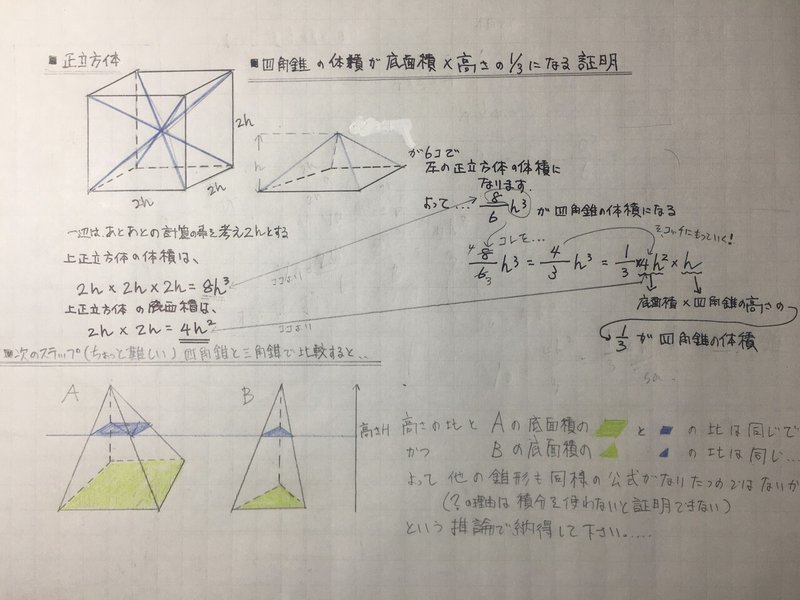「四角錐の公式」の画像ギャラリー、詳細は各画像をクリックしてください。

 でした．これは三角錐でも四角錐でも，円錐でも使える公式です． この式に登場する \(\frac{1}{3}\)って何なの？という話をします． 三角形の面積と一緒？？ 上に書いた錐の体積の公式とよく似た形の公式があることに気がつくでしょうか？ シンプソンの公式は単純な積分のみならず、考え方次第では体積を求めるのにも使えます。 今回はその例をいくつか紹介します。 Ⅰ 体積への拡張 Ⅱ 三角柱の体積 Ⅲ 円錐の体積 Ⅳ 四角錐台の体積 Ⅰ 体積への拡張 一応最初なので、シンプソンの公式を復習しておきましょう。

Incoming Term: 四角錐の公式,